線分ABを一辺とする正方形を作図しなさいという問題の解き方を調べたのですが、動画の解説しか見つからなかったので、健忘録も兼ねて記しておきます。コンパスを使います。
もくじ
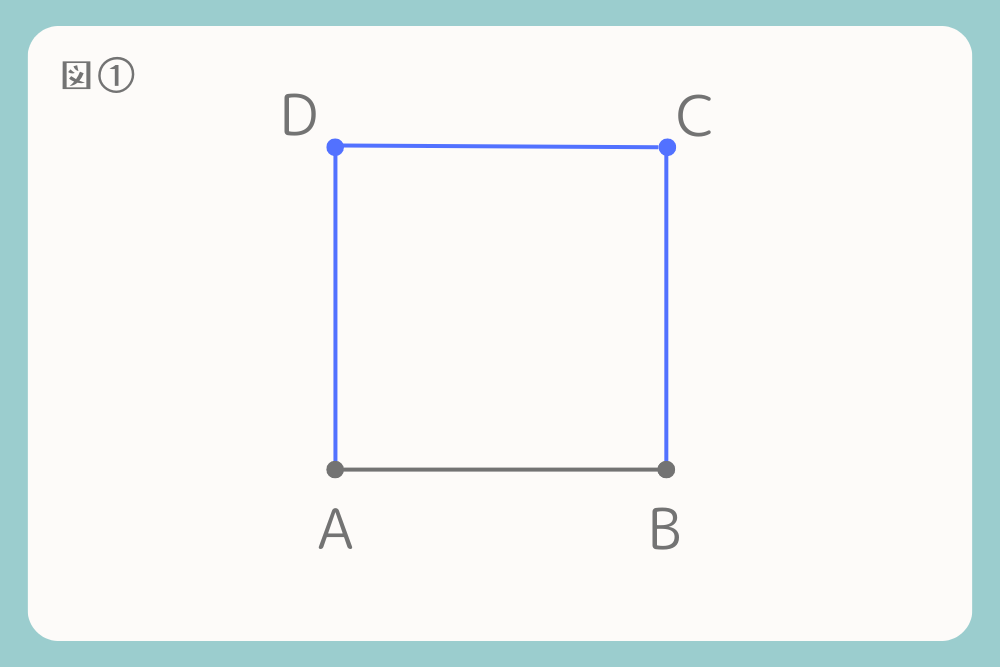
【問題】線分ABを一辺とする正方形を作図しなさい。
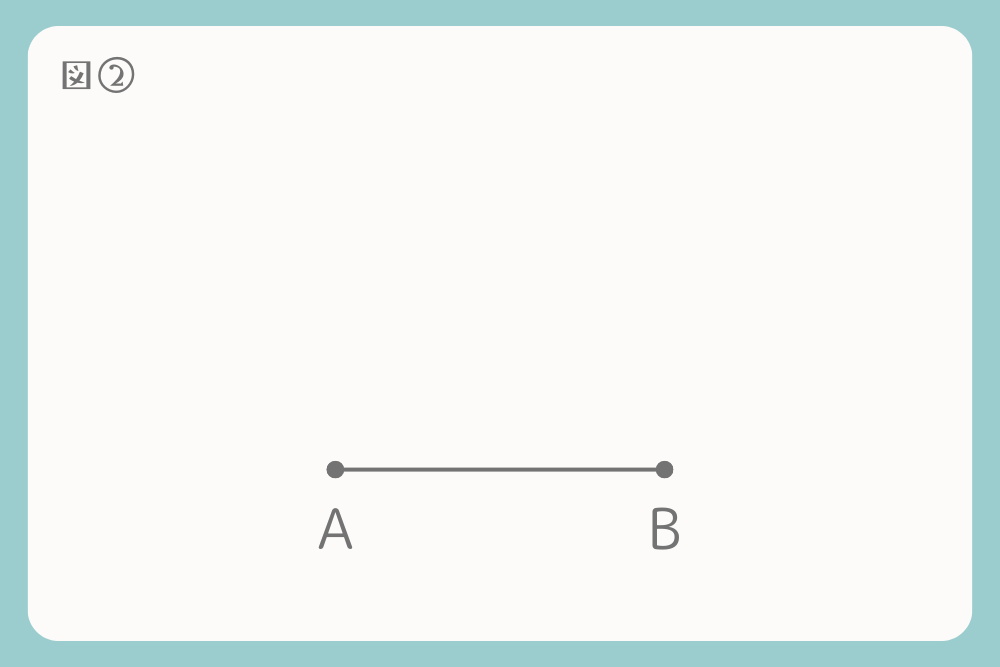
1)点Bの線を伸ばします
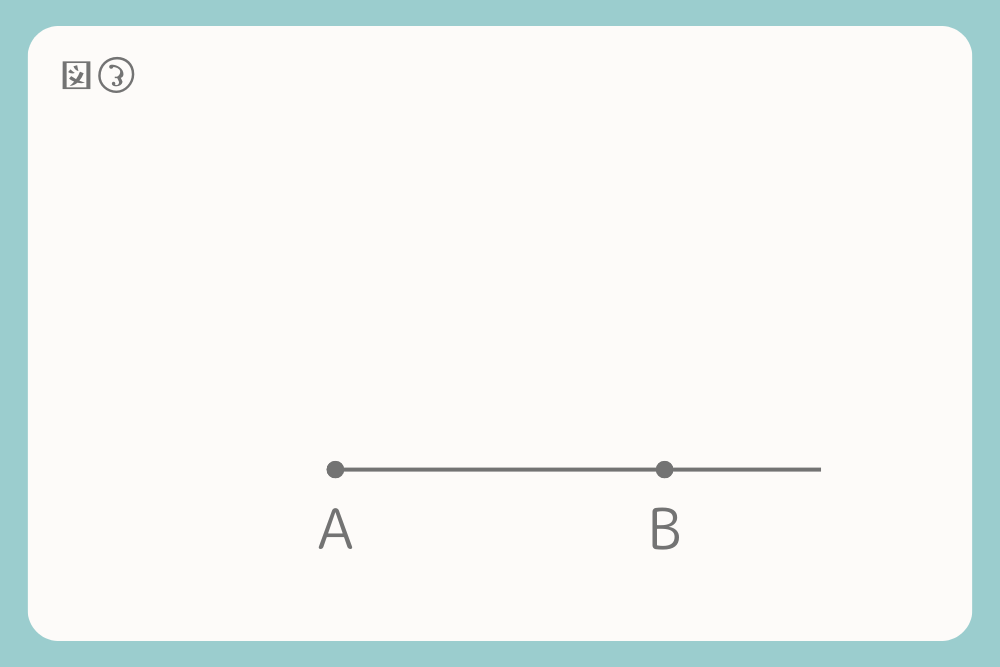
2)垂線を作図します
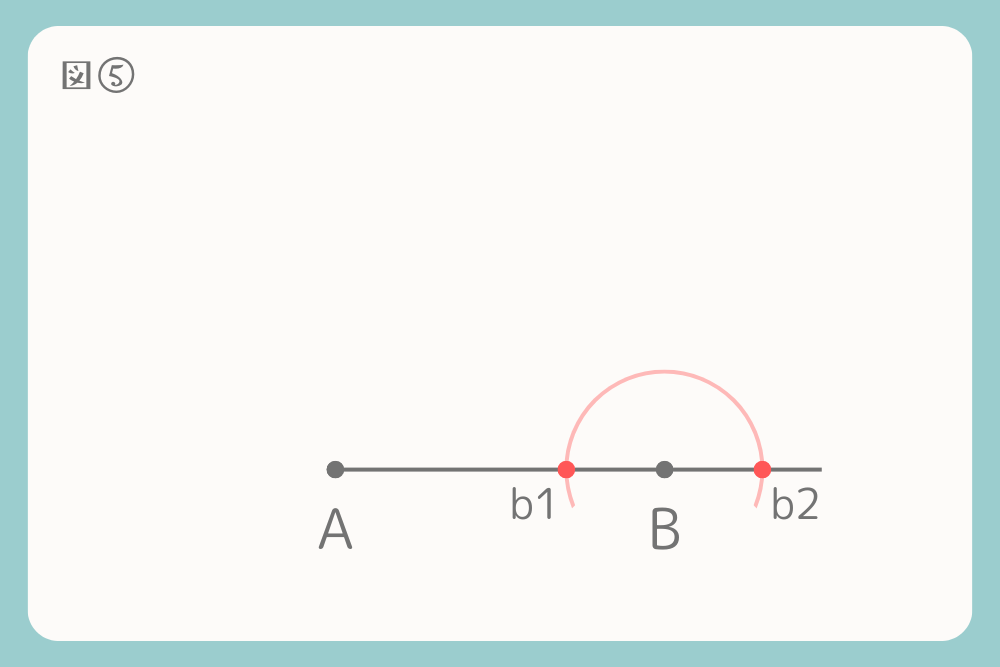
点Bを中心としてコンパスで半円を描きます。
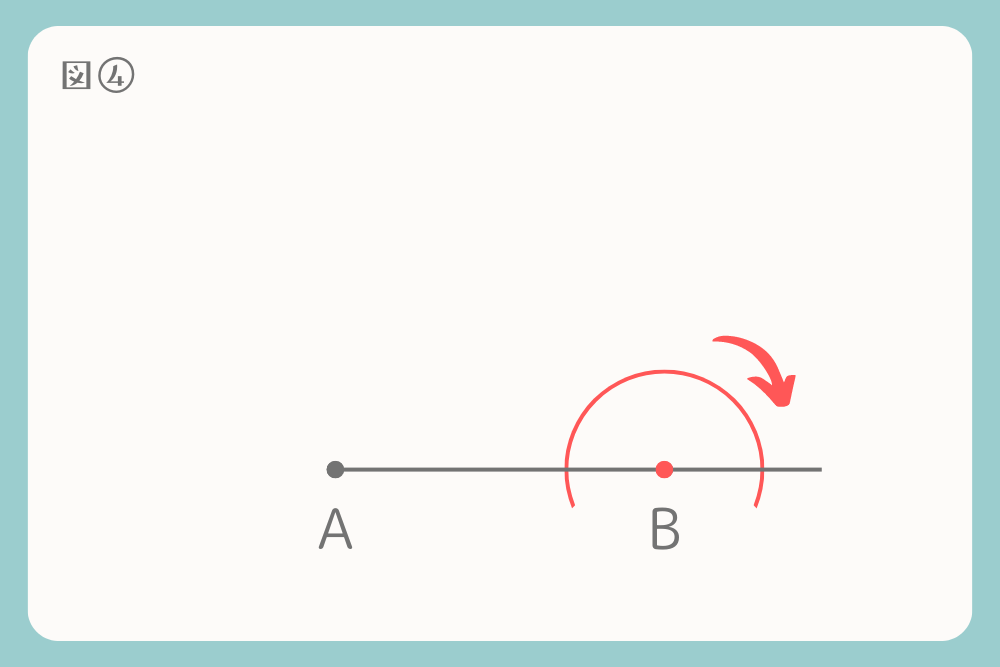
線上とコンパスで描いた交点をそれぞれb1、b2とします。
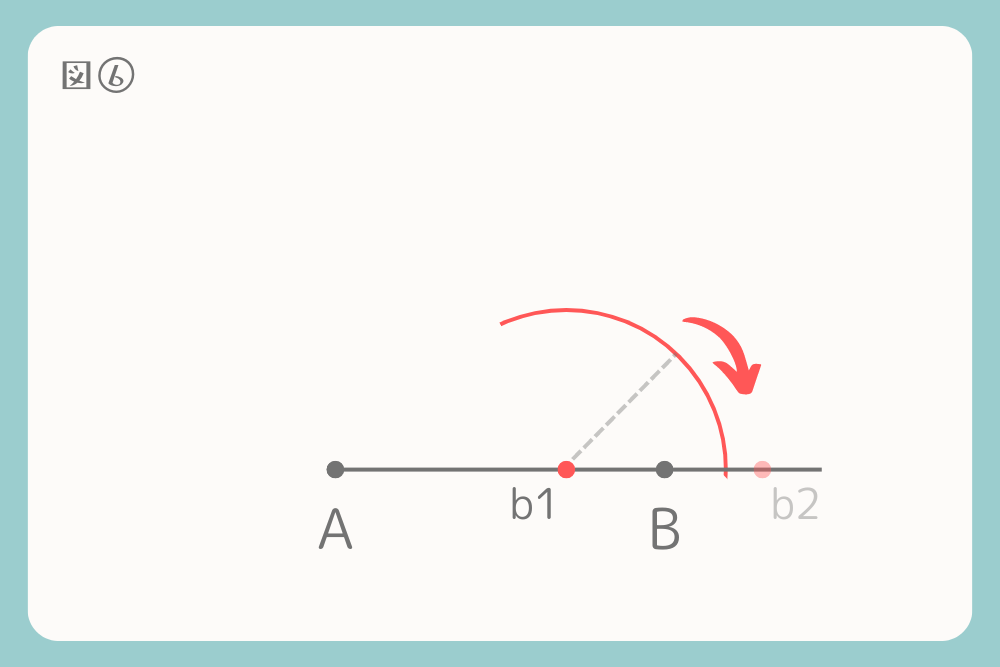
コンパスを先ほどより少し開き、b1から半円を描きます。
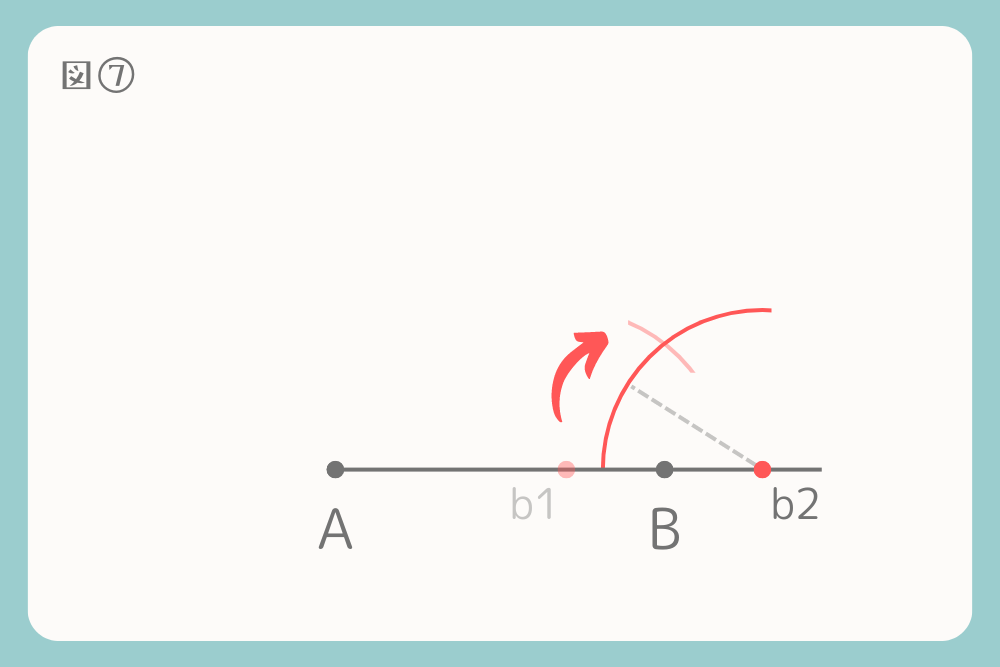
コンパスはそのままで、b2から半円を描きます。
点Bの上下でコンパスが重なるような円を描くイメージです。
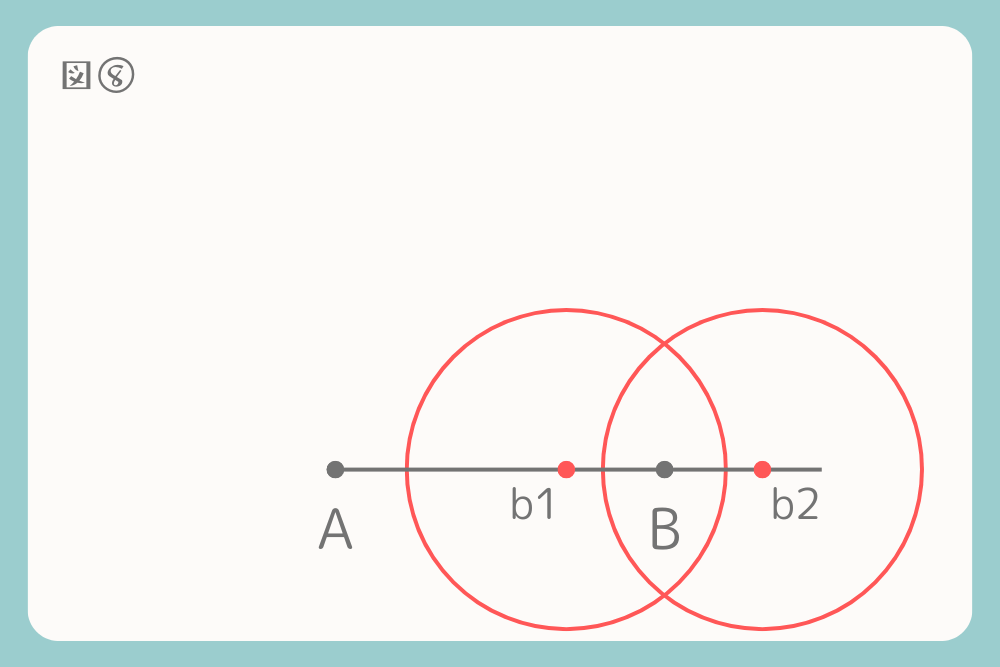
b1とb2を中心とした二つの円の重なっている点をPとQとします。
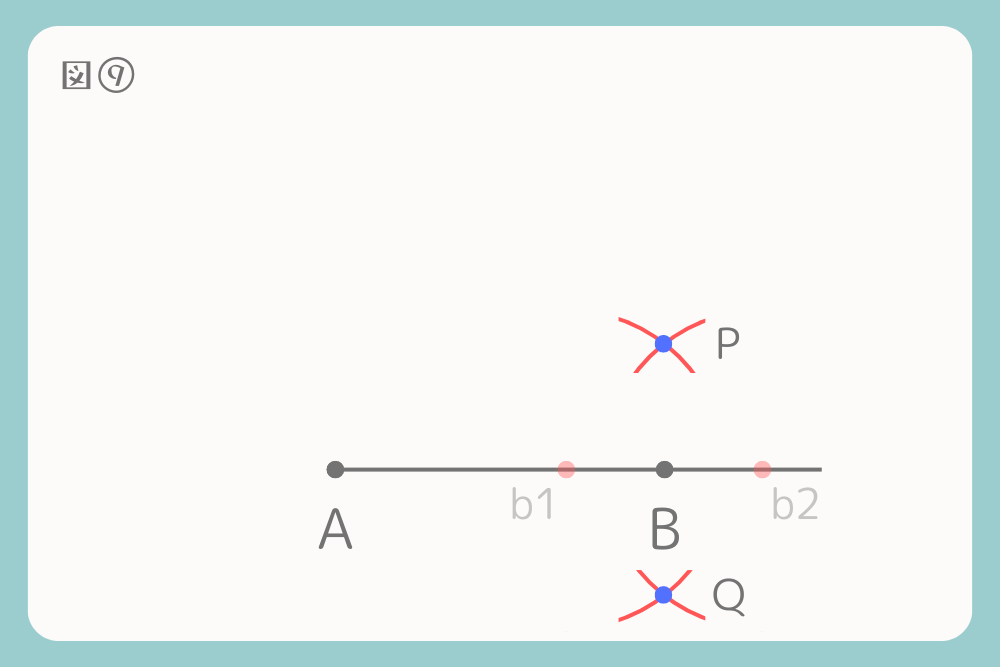
PとQを結ぶ線をひきます。
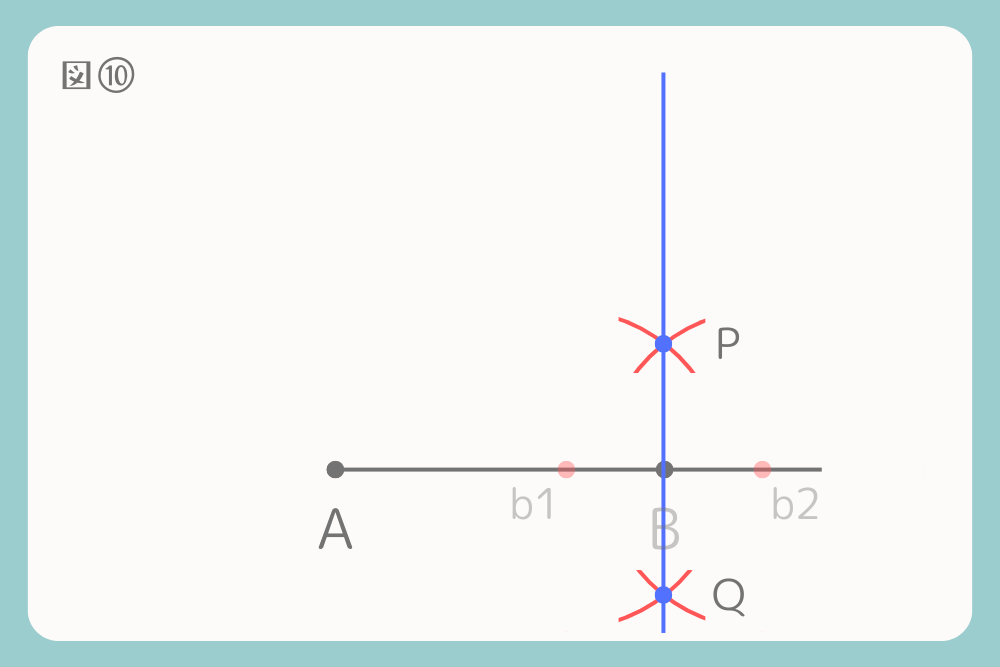
3)線分ABを半径として中心点からコンパスで円を描きます
線分ABを半径として中心点Bからコンパスで円を描きます。コンパスの円と垂線PQ上で交差した点を点Cとします。
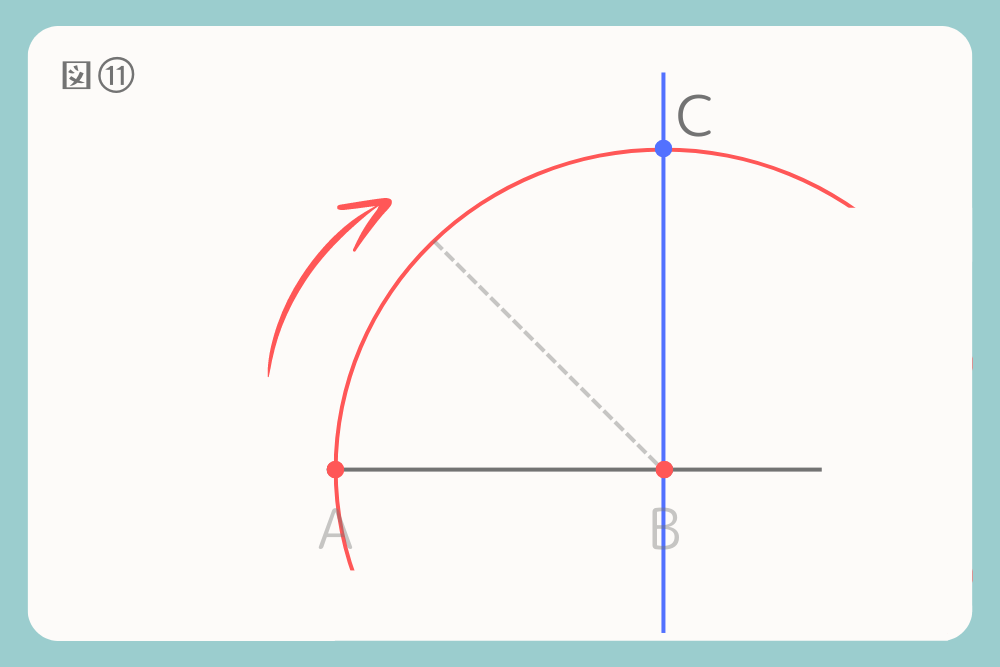
次に、線分ABを半径として中心点Aからコンパスで円を描きます。
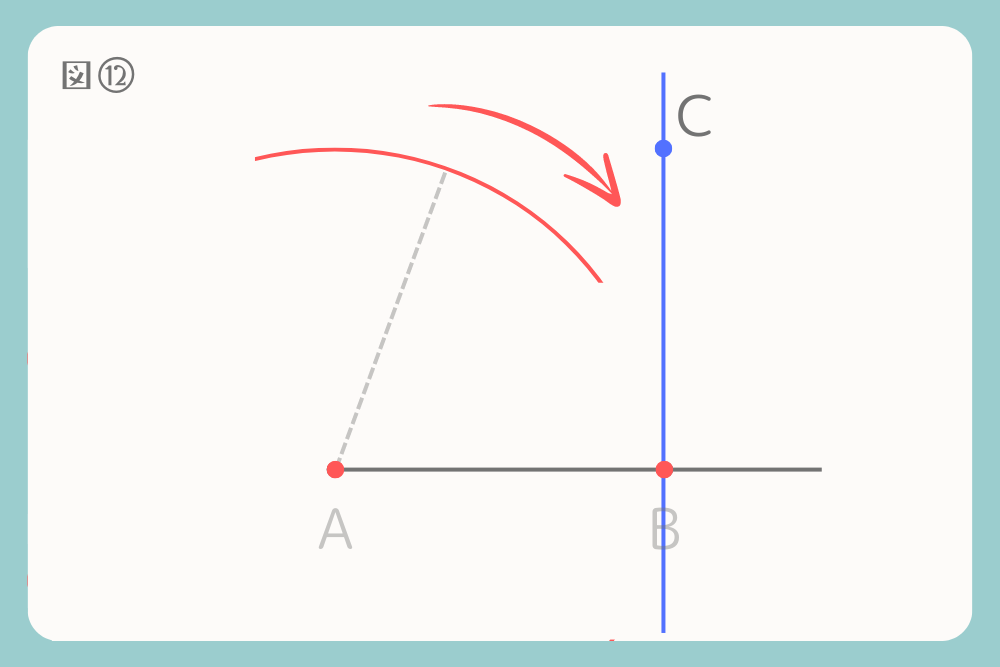
そのまま、線分ABを半径として中心点Cからコンパスで円を描きます。中心点Aの円と中心点Cの円の交点を点Dとします。
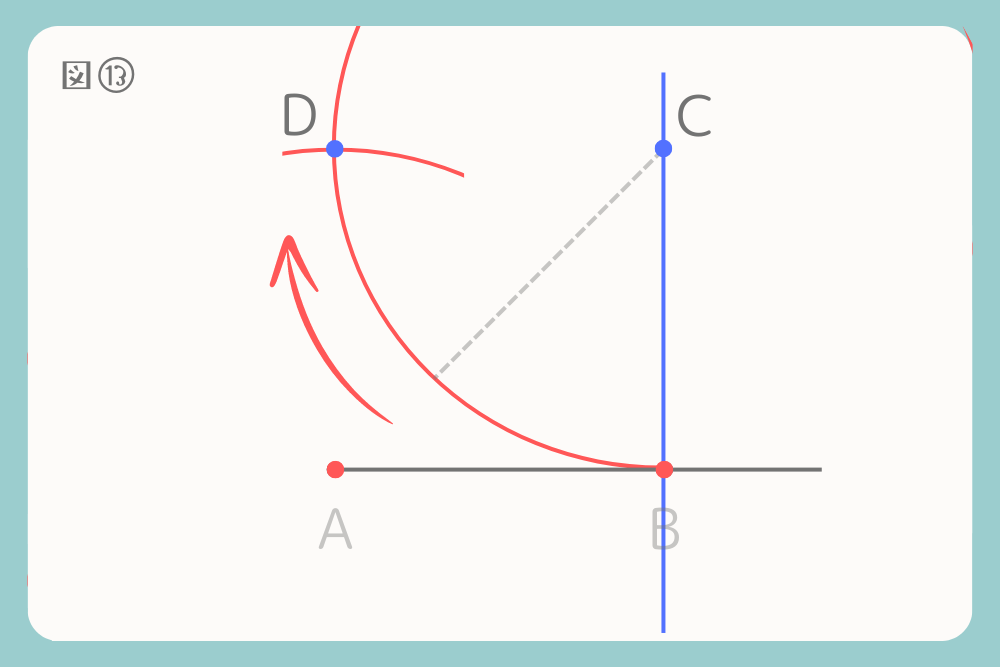
4)ABCDを線で結びます
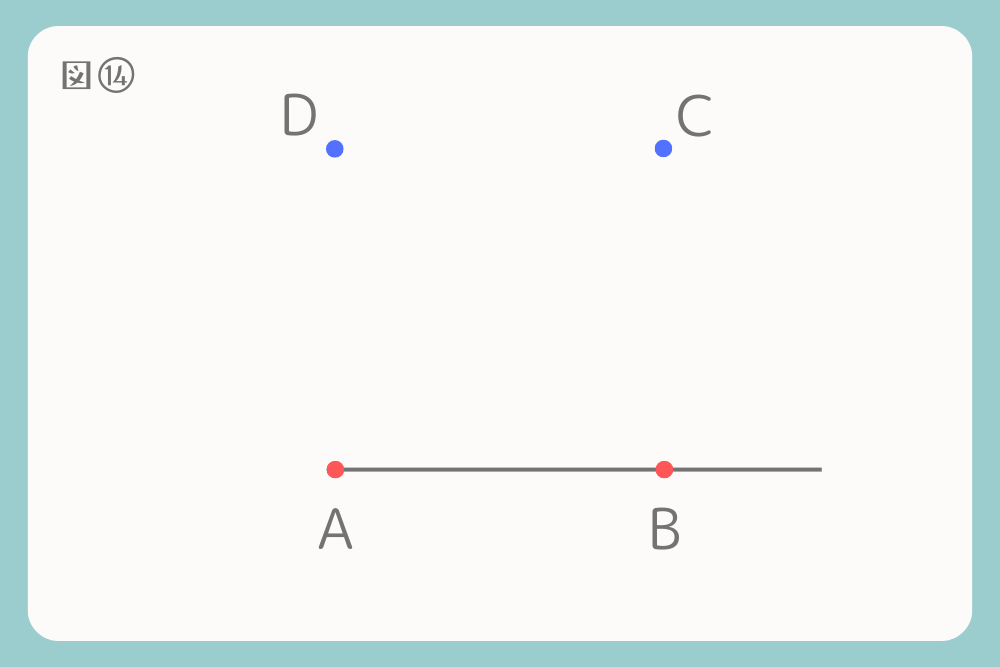
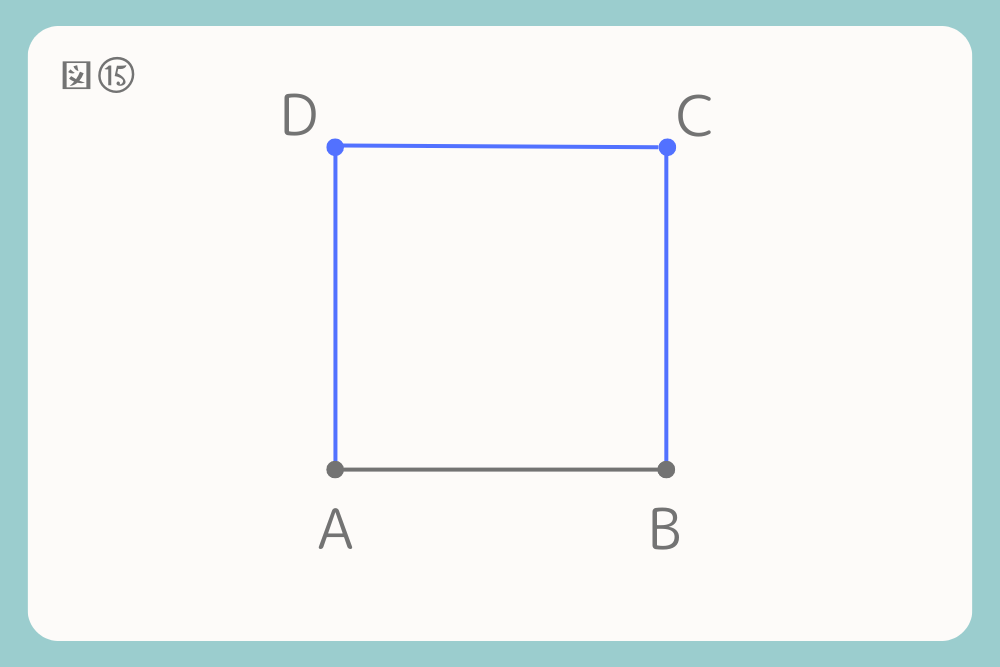
完成です。線分ABを一辺とする正方形が作図できました。
文字で説明されていた作図方法が理解できなくて動画の解説を参考にしました。動画を見たほうが早いかもしれませんが、文字情報が必要な方の参考になればと思いまとめてみました。お役に立てましたら嬉しいです。
お読みいただきありがとうございます。(*'ω'*)
良ければ、人生の応援メッセージをランダムで表示するボタンもどうぞ
