ある数を分数で割ると値が大きくなる…例えば、24÷\(\frac{1}{4}\)=96になります。感覚的には「分数で割ると小さくなるのでは？」というイメージだったので、答えが割られる数より増えることが不思議でした。でも、理解できたら面白かったので、その理由をご紹介します。
もくじ
本の残りのページ数を読んだ割合で割ると本全体のページ数が求められる
中学入試問題の「相当算」を解いていたとき、ある本の残りのページ数を読んだ割合で割ると本全体のページ数が求められる仕組みがわからず混乱しました。
次のような問題です。
例題：
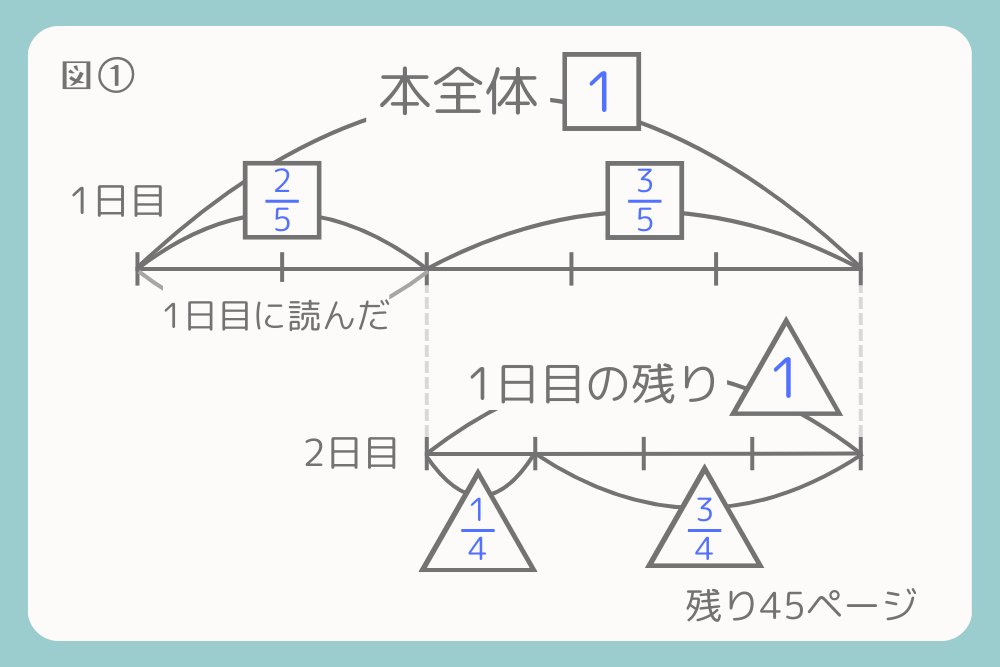
ある本を、1日目は全体のページ数の\(\frac{2}{5}\)を読み、2日目は残りのページ数の\(\frac{1}{4}\)を読むと、残りは45ページでした。この本は全体で何ページでしょうか？
線分図を使って考えます。
解説：
まず、2日目の残りのページ数45ページを2日目の残りの割合の\(\frac{3}{4}\)で割ると、1日目の残りのページ数が求められます。
\(45÷\frac{3}{4}=60\)
んんん？？？？？ なんで、いきなり60ページに増えるの？
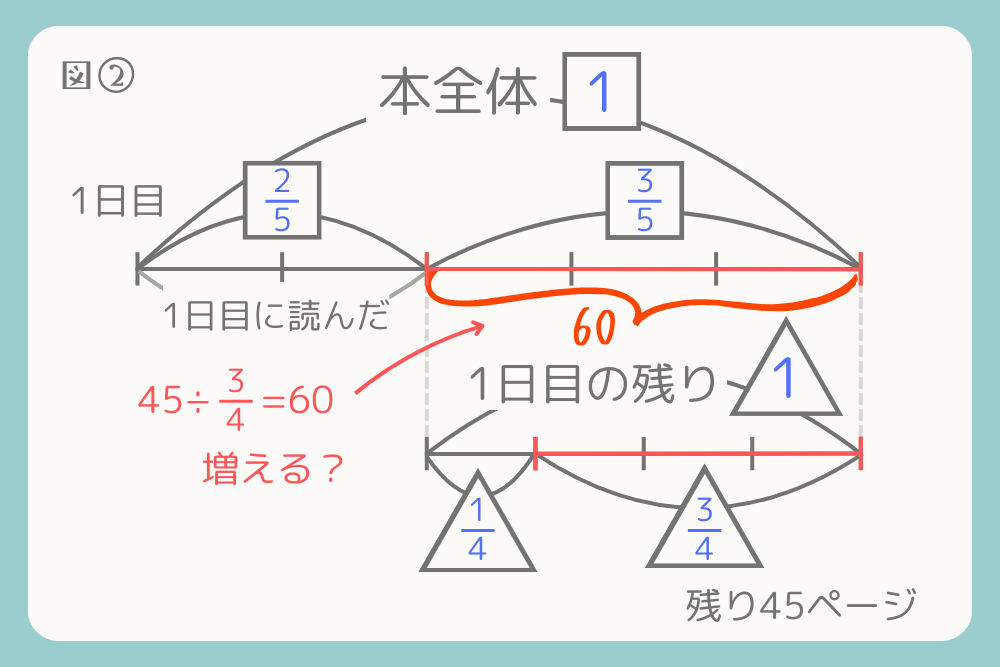
なぜこの計算になるの？
先生に教えていただいたところ、次のような手順になります。
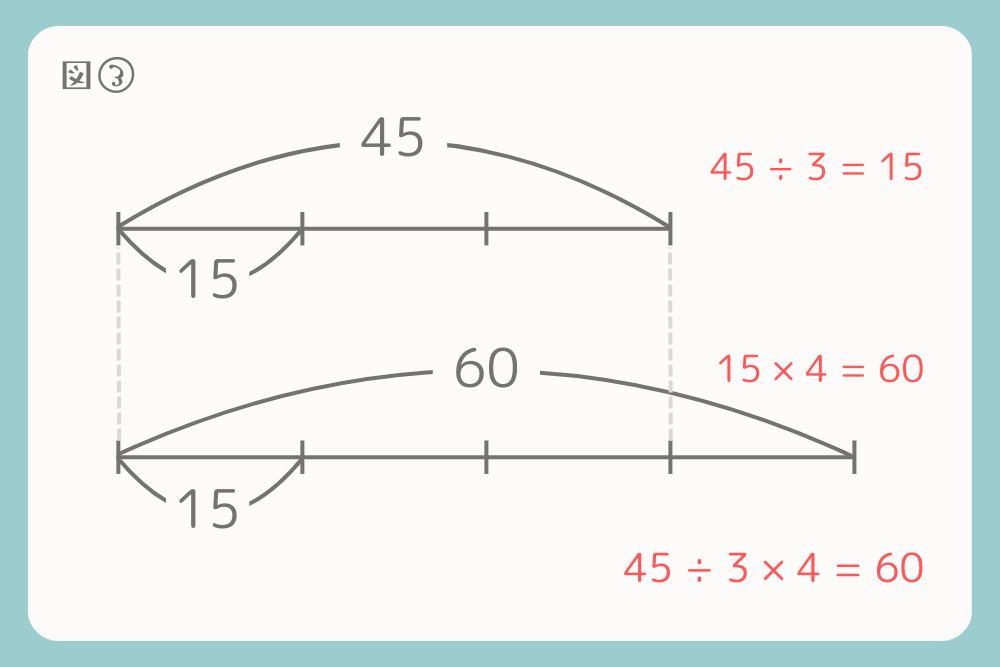
① 45を3で割る
\(45÷3=15\)
② 15を4倍にする
\(15×4=60\)
つまり、次のような計算になります。
\(45÷3×4=60\)
分数の割り算の意味
おおおおお？
分数の割り算は「ひっくり返して掛ける」と覚えますよね。つまり、
\(45÷\frac{3}{4}=45×\frac{4}{3}=60\)
結果的に、次のように考えられます。
\(45÷3×4=60\) ですね！
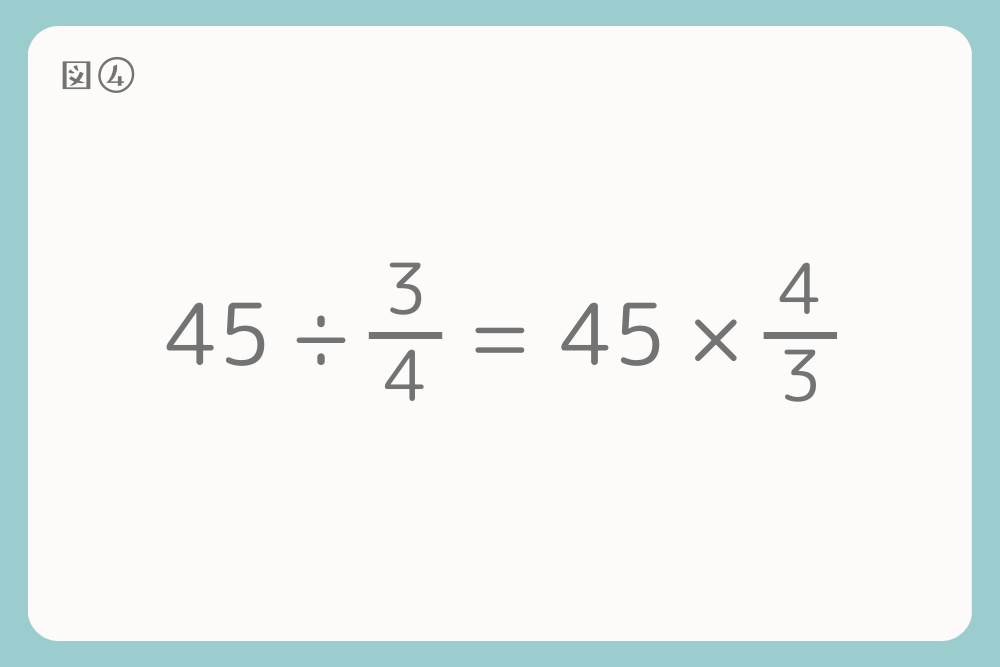
まとめ
「分数で割る」というのは、その分数の逆数を掛けるということ。例えば、
\(45÷\frac{3}{4}=45×\frac{4}{3}\)
つまり、分数\(\frac{4}{3}\)は1より大きな数（\(1.33…\)）なので、掛けた結果、値が大きくなります。
分数で割ると値が大きくなるのは、「逆数を掛けるから」と考えると理解しやすいですね。
例題の答え
例題：ある本を、1日目は全体のページ数の\(\frac{2}{5}\)を読み、2日目は残りのページ数の\(\frac{1}{4}\)を読むと、残りは45ページでした。この本は全体で何ページでしょうか？
まず、2日目の残りのページ数45ページを2日目の残りの割合の\(\frac{3}{4}\)で割って、1日目の残りのページ数を求めます。
\(45÷\frac{3}{4}=60\)
そして、1日目の残りのページ数60ページを1日目の残りの割合の\(\frac{3}{5}\)で割ると、本全体のページ数が求められます。
\(60÷\frac{3}{5}=100\)
答え：100ページ
ある数（自然数）を割って値が増える分数は？
1)分数が1未満の場合（真分数）
| 例 | \(6÷\frac{2}{3}\) |
| 計算手順 | \(6÷\frac{2}{3}=6×\frac{3}{2}=\frac{18}{2}=9\) |
真分数（分子が分母より小さい分数）で割ると、必ず数が増えます。
これは、真分数の逆数が 1 より大きい数になるためです。
2)分数が 1 を超える場合 (仮分数)
| 例 | \(6÷\frac{5}{4}\) |
| 計算手順 | \(6÷\frac{5}{4}=6×\frac{4}{5}=\frac{24}{5}=4.8\) |
仮分数（分子が分母より大きい分数）で割ると、元の数より 小さくなります。逆数が 1 未満だからです。
成り立つ条件
- 増える: 分数が 1 未満（真分数）の場合
- 変わらない: 分数が ちょうど 1 の場合
- 減る: 分数が 1 より大きい（仮分数）の場合
よって、自然数を分数で割ったときに値が増えるのは、 分数が 1 未満のときだけ 成り立ちます。
どうしても分数で割ると値が小さくなるイメージだったのですが、分数の割り算はひっくり返して掛けるのですから値は大きくなるのですね！
分数の割り算はひっくり返して掛けるのはなぜか？は、こちらのサイトのスライドが最高に分かりやすかったのでぜひご覧ください！
参考：「分数の割り算のやり方」：https://keisan.otona-juku.com/02026fraction-division/
お読みいただきありがとうございました。
良ければ、人生の応援メッセージをランダムで表示するボタンもどうぞ
